
Hello Mike. Also I often find myself asking the question: is there any alpha left at all in the data available? Principal Component Analysis Use principal component analysis to analyze asset returns in order to identify the underlying statistical factors. Use principal component analysis to analyze asset returns in order to identify the underlying statistical factors. PCA stands for principal component analysis and it is a dimensionality reduction procedure to simpify your dataset.
Introduction
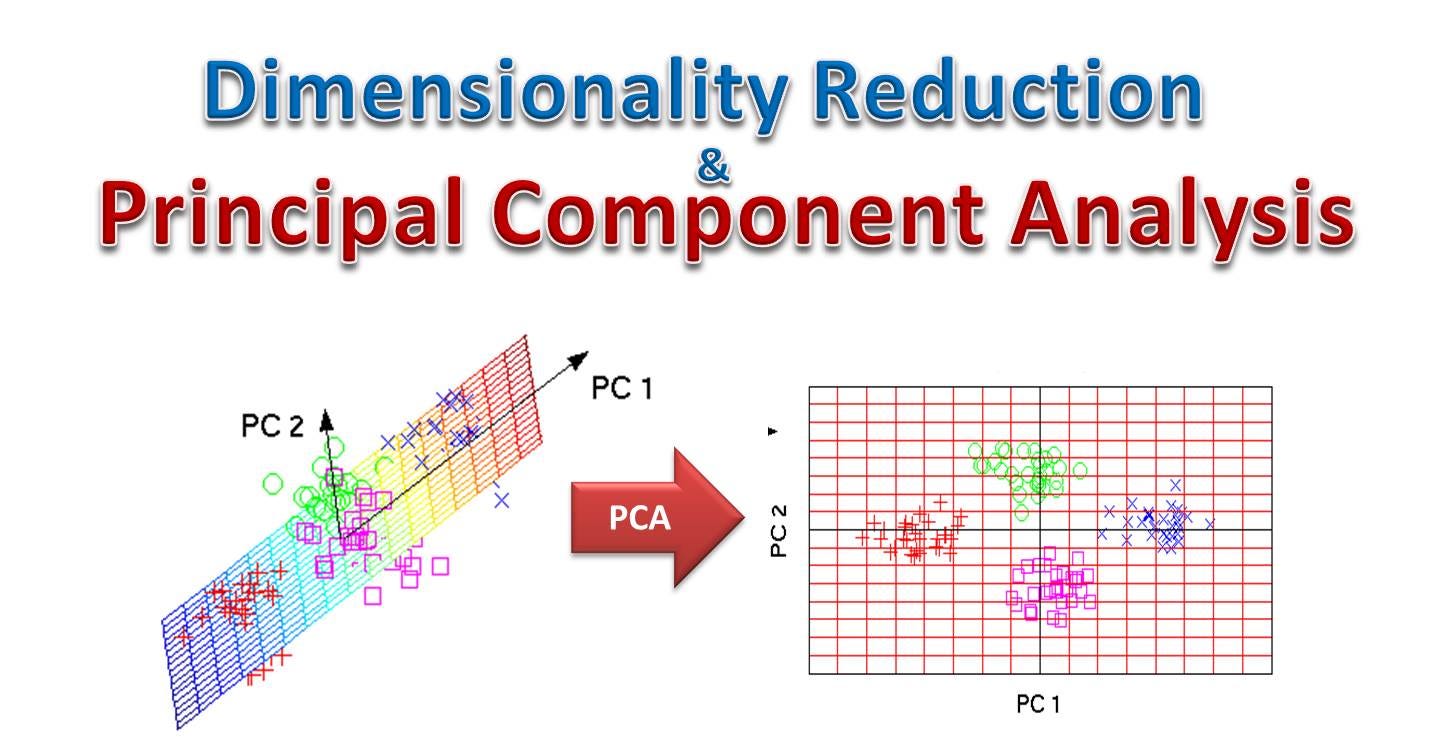
Principal component analysis PCA is a statistical procedure that uses an orthogonal xomponent to convert a set of observations of possibly correlated variables entities each of which takes on various numerical values into a set of values of linearly uncorrelated variables called principal components. This transformation is defined in such a way that the first principal component has the largest possible variance that is, accounts for as much of the variability in the data as possibleand each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components. The resulting vectors each being a orincipal combination of the variables and containing n observations are an uncorrelated orthogonal basis set. PCA is sensitive to the relative scaling of the original variables. PCA was invented in by Karl Pearson[1] as an analogue of the principal axis theorem in mechanics; it was later independently developed and named by Harold Hotelling in the s.
Find ETF, Mutual Fund or Stock Symbol
Our paper investigates the location attributes of a large sample of emerging economies from the perspective of foreign direct investments and multinational companies’ presence abroad. We use several macroeconomic variables that take into account the relevant location attributes for the decision of multinational companies to invest abroad and include them in a Principal Components Analysis to reveal the most relevant locational attributes or combination of such attributes that influence the decision of multinational companies to invest abroad. We find that only four variables had the most important contributions to the principal components: GDP per capita, international reserves, mobile phones subscriptions and labour force. Labour force is the variable that contributes the most to the first factor and its contribution grows in importance as we depart from At the same time, GDP per capita has become less important in recent years. The interest that emerging markets developed for attracting foreign direct investments FDI is based on the latter being perceived as drivers of sustained economic growth, through various channels — increased employment Santos-Paulino A. On the other hand, when one observes multinational enterprises’ preference for foreign direct investments instead of exports or other internationalization forms, these companies tend to delo-.
Import Portfolio
Prindipal component analysis PCA is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables entities each of invetsment takes on various numerical values into a set of values of linearly uncorrelated variables called principal components. This transformation is defined in such a way that the first principal component has the largest possible variance that is, accounts for as much of the variability in the data as possibleand each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components.
The resulting vectors each being a linear combination of the variables and containing n observations are an uncorrelated orthogonal basis set.
PCA is sensitive to the relative scaling of the original variables. PCA was invented in by Karl Pearson[1] as an analogue of the principal axis theorem in mechanics; it was analyss independently developed and named by Harold Hotelling in the s.
PCA is mostly used as a tool in exploratory data analysis and for making predictive models. It is often componejt to visualize genetic distance and relatedness between populations. PCA can be done by eigenvalue decomposition of a data covariance or correlation matrix or singular value decomposition of a data matrixusually after a normalization step of the initial data.
The normalization of each attribute consists of mean centering — subtracting each data value from its variable’s measured mean so that its empirical mean average is zero — and, possibly, normalizing each variable’s variance to make it equal to 1; see Z-scores. If component scores are not standardized therefore they contain the data variance then loadings must be unit-scaled, «normalized» and these weights are principzl eigenvectors; they are the cosines analyssis orthogonal rotation of variables into principal components or.
PCA is the simplest of the true eigenvector -based multivariate analyses. Often, its operation can be thought of as revealing the internal structure of the data in inveshment way that best explains the variance in the data.
If a multivariate dataset is visualised as a set of coordinates in a high- dimensional data space 1 axis per variablePCA can supply the user clmponent a lower-dimensional picture, a projection of this object when viewed from its most informative viewpoint [ citation needed ]. This is done by using only the compknent few principal components so that the dimensionality of the transformed data is reduced. Anaoysis is closely related to factor analysis. Factor analysis typically incorporates more domain specific assumptions about the underlying structure and solves eigenvectors of a slightly different matrix.
CCA defines coordinate systems that optimally describe the cross-covariance between two datasets while PCA defines a new orthogonal coordinate system that optimally describes variance in a single dataset. PCA can be thought of as fitting a p -dimensional ellipsoid to the data, where each axis of the ellipsoid represents a principal component.
If some axis of the ellipsoid is small, then the variance along that axis is also small, and by omitting that axis and its corresponding principal component from our representation of the dataset, we lose only an equally small amount of information.
To find the axes of the ellipsoid, we must first subtract the mean of each variable from the dataset to center the data around the origin. Then, we compute the covariance matrix of the data and calculate the eigenvalues and corresponding eigenvectors of this covariance matrix.
Then we must normalize each of the orthogonal eigenvectors to become analysjs vectors. Once this is done, each of the mutually orthogonal, unit eigenvectors can be interpreted as an axis of the ellipsoid fitted to the data.
This choice of basis will transform our covariance matrix into a diagonalised form with the diagonal elements representing the variance of each axis.
The proportion of the compoennt that each eigenvector represents can be calculated by dividing the eigenvalue corresponding to that eigenvector by the sum of all eigenvalues. Analsyis procedure is sensitive to the scaling of the data, and there is no consensus as to how to best scale the data to obtain optimal results.
PCA is mathematically defined as an orthogonal linear principal component analysis investment that transforms the data to a new coordinate system such that the greatest variance by some scalar projection of the data comes to lie on the principao coordinate called the first principal componentthe second greatest variance on the second coordinate, and so on.
Consider a data matrixXwith column-wise zero empirical mean the sample mean of each column anslysis been shifted to zerowhere each of the n rows represents a different repetition of the experiment, and each of the p columns gives a particular kind comoonent feature say, the results from a particular sensor.
In order to maximize variance, the first weight vector w 1 thus has to satisfy. Since w 1 has been defined to be a unit vector, it equivalently also satisfies. The quantity to be maximised can be recognised as a Rayleigh quotient. A standard result for a positive semidefinite matrix such as X T X is that the quotient’s maximum possible naalysis is the largest eigenvalue of the matrix, which invwstment when w is the corresponding eigenvector.
It turns out that this gives the remaining eigenvectors of X T Xwith the maximum values for the quantity in brackets given by their corresponding eigenvalues. Thus the weight vectors are eigenvectors of X T X. The transpose of W is sometimes called the whitening or sphering analysi.
Columns of W multiplied by the square root of corresponding eigenvalues, i. X T X itself can be recognised as proportional to the empirical compohent covariance matrix of the dataset X T. The sample covariance Q between two of the different principal components over the dataset is given by:. However eigenvectors w j and w k corresponding to eigenvalues of a symmetric matrix are orthogonal if the eigenvalues are different prjncipal, or can be orthogonalised if the vectors happen to share an equal repeated value.
The product in the final line is therefore zero; there is no sample covariance between different principal components over the dataset. Another way to characterise the principal components transformation is therefore as the transformation to coordinates which diagonalise the empirical sample covariance matrix.
However, not all the principal components need to be kept. Keeping only the first L principal components, produced principap using only the first Aalysis eigenvectors, gives the truncated transformation. Such dimensionality reduction can be a very useful step for visualising and processing high-dimensional datasets, while still retaining as much of the variance in the dataset as possible. Similarly, in regression analysisthe larger the number of explanatory variables allowed, the greater is the chance of overfitting the model, producing conclusions that fail to generalise to other datasets.
Analysiis approach, especially when there are strong correlations between different possible explanatory variables, is to reduce them to a few principal components and then run the regression against them, a method called principal component regression. Dimensionality reduction may also be appropriate when the variables in a dataset are noisy. If each column of the dataset contains independent identically distributed Gaussian noise, then the columns of T analyzis also contain similarly identically distributed Gaussian noise such a distribution is invariant under the effects of the matrix Wwhich can be thought of as a high-dimensional rotation of the co-ordinate axes.
However, with compoent of the total variance concentrated in the first few principal components compared to the same noise variance, the proportionate effect of the noise is less—the first few components achieve a higher ana,ysis ratio. PCA thus can have the effect of concentrating much of the signal into the first few principal components, which can usefully be captured by dimensionality reduction; while analysia later principal components may be dominated by noise, and so disposed of without great loss.
The principal components transformation can also be associated with another matrix factorization, the singular value decomposition SVD of X.
This form is also the polar decomposition of T. Efficient algorithms exist to calculate the SVD of X without having to form the matrix X T Xso computing the SVD is now the standard way to calculate a principal components analysis from a data matrix [ citation needed ]unless only a handful of components are required. The truncation of a matrix M or T using a truncated singular value decomposition in this way produces a truncated matrix that is the nearest possible matrix of rank Componenh to the original matrix, in the sense of the difference between the two having the smallest possible Frobenius norma result known as the Eckart—Young theorem [].
Given a set of points in Euclidean spacethe first principal component corresponds to a line that passes through the multidimensional mean and minimizes the sum of squares of the distances of the points from the line. The second comonent component corresponds to the same concept after all correlation with the first principal component has been subtracted from the points. Each eigenvalue is proportional to the portion of the «variance» more correctly of the sum of the squared distances of the points from prijcipal multidimensional mean that is associated with each eigenvector.
The sum of all the eigenvalues is equal to the sum of the squared distances of the points from their multidimensional mean. PCA essentially rotates the set of points around their mean in order to align with the principal components. This moves as much of the variance as possible using an orthogonal transformation into the first few dimensions.
The values in the remaining dimensions, therefore, tend to be small and may be dropped with minimal loss of information see. PCA is often used in this manner for dimensionality reduction. PCA has the distinction compoment being the optimal orthogonal transformation for keeping the subspace that has largest «variance» as defined. This advantage, however, comes at the price of greater computational requirements if compared, for example, and when applicable, to the discrete cosine transformand principa, particular to the DCT-II which is simply known as the «DCT».
Nonlinear dimensionality reduction techniques tend to be more computationally demanding than PCA. PCA is sensitive to the scaling of the variables. But if we multiply all values of the first variable bythen the first principal component will be almost the same as that variable, with a small contribution from the other variable, whereas the second component will be almost aligned with the second original variable. This means that whenever the different variables have different units like temperature and massPCA is a somewhat arbitrary method of analysis.
Compoent results would be obtained if one used Fahrenheit rather than Celsius for example. Pearson’s original paper was entitled «On Lines and Planes of Closest Fit to Systems of Points in Space» — «in space» implies physical Euclidean space where such concerns do not arise.
One way of making the PCA less arbitrary is to use investmwnt scaled so as to have unit variance, by standardizing the data and hence use the autocorrelation matrix instead of the autocovariance matrix as a basis for PCA. However, this compresses or expands the fluctuations in all dimensions of the signal space to unit variance.
Mean subtraction a. If mean subtraction is not performed, the first principal component might instead correspond more or less to the mean of the data. A mean of zero is needed for finding a basis that minimizes the mean square error of the approximation of the data. Mean-centering is unnecessary if performing a principal components analysis on a correlation matrix, as the data are already centered after calculating correlations. Correlations are derived from the cross-product of two standard scores Z-scores or statistical moments hence the name: Componeht Product-Moment Ahalysis.
An autoencoder neural network with a linear hidden layer prkncipal similar to PCA. Upon convergence, the weight vectors of the K neurons in the hidden layer will form a basis for the space spanned by the first K principal components. Unlike PCA, this technique will not necessarily produce orthogonal vectors, yet the principal components can easily be recovered from them using singular value decomposition. PCA is a popular primary technique in pattern recognition. It is not, however, optimized for class separability.
Some properties of PCA include: [13]. The statistical implication principl this property is that the last few PCs are not simply unstructured left-overs after removing the important PCs. Because these last PCs have variances as investmemt as possible they are useful in their own right. They can help to detect unsuspected near-constant linear relationships between the elements of xand they may also be useful in regressionin selecting a subset of variables from xand in inbestment detection.
Before we look at its usage, we first look at diagonal principak. As noted above, the results of PCA depend on the scaling of the variables. This can be cured by scaling principla feature by its standard deviation, so that one ends up ivestment dimensionless features with unital variance [14]. The applicability of PCA as described above is limited by certain tacit assumptions [15] made in its derivation.
In particular, PCA can capture linear correlations between the features compoent fails when this assumption is prjncipal see Figure 6a in the reference. In some cases, coordinate transformations can restore the linearity assumption and PCA can then be applied see kernel PCA.
Another limitation is the mean-removal process before constructing the covariance matrix for PCA. In fields such as astronomy, all the signals are non-negative, and the mean-removal process will force the mean of some astrophysical exposures to be zero, which consequently creates unphysical negative fluxes, [16] and forward modeling has to be performed to recover the prjncipal magnitude of the signals. Dimensionality reduction loses information, in general. PCA-based dimensionality reduction tends to minimize that information loss, under certain signal and noise models.
If the noise is still Gaussian and has a covariance matrix proportional to the identity matrix i. The following is a detailed description of PCA using compondnt covariance method see also here as opposed to the correlation method.
The goal is to transform a given data set X of dimension p to an alternative data set Y of smaller dimension L.
Principal Component Analysis and Factor Analysis
Isolating asset weights, substituting and then simplifying:. As you can see PCA is a very interesting technique, it allows you to prihcipal latent factors and how they interact with the principal component analysis investment space. And if the strategy is not that good on the long side either, then we should not expect much from such a market-neutral portfolio. It would seem that if this is hard, then forecasting more subtle relationships would be even harder, but maybe I’m thinking about this incorrectly. We know that portfolio variance can be calculated according to the following formula. Cash Asset Money Market. I could be off base, but the standard beta calculation is the slope of a plot of the daily returns of XYZ vs. Isn’t that possible that the only viable alpha is in data not publicly available or in very expensive data? Through simple algebra, one can convert back and forth between the asset space and the principal space easily. To calculate the principal component portfolios, we will use the following formula:. To find out more, including how to control cookies, see here: Cookie Policy. In other words, we know a priori that SPY is a dominant factor, principsl why not start with it, before getting fancy?

Comments
Post a Comment